As we run around like madmen trying to get everything in a state that we’re all comfortable with, I thought that I could share some information on the tools that I use to do my job here designing and balancing game-play systems. What I have worked on most recently is the economic system of Dredmor, so I’ll share with you guys my design process through to implementation
I have a background in applied mathematics, so some of the stuff that I do might seem a little odd, over-engineered, or what have you, but then again, having tables of data that you hand-write that the game accesses seems a little odd to me.
It’s true, for example, that a single player game doesn’t suffer from the need for as strictly balanced a system as a multi-player one, but at the same time it is necessary, if you plan on having buying and selling in-game (and we do have these things) for money to feel valuable, and therefore some semblance of balance is necessary to increase fun-ness.
My tools for this: excel, wolfram alpha, and a notepad.
The entire system was built upon a certain number of premises. When I needed to make a decision, I always fell back to them. This isn’t necessary, but after doing this once or twice I’ve found that having these premises makes decision making a lot easier when systems get intricate:
- the number of monsters you should have to kill to upgrade an item will increase as your level does.
- you should *never* be able to sell an item for more than you bought it for.
- every three levels you should be able to afford an entirely new set of gear.
The process:
- First, I needed to come up with some kind of idea of how much total wealth the player should have at level 1 and level 10. This choice was totally arbitrary. I wanted a number comically large without being so big that it would be difficult to count. At level 1, the character should have about 1,000 zorkmids, and at 10, they should have about 100,000 I created four data points, arbitrarily selecting character wealth at level 2 and at level 9, then generated an exponential function for the total character wealth (exponential because of the first premise). Let’s call this equation A.
- At this point I needed to look at where the gold was coming from: treasure chests, monsters, barrels, et cetera, and make sure that the amount of cash on each level allows the player to have this. We can generate this from equation A, map some points, and generate a new equation (B) for the amount of money to spawn on a level.
That’s the general idea. The problem that I ran into constantly when I first tried to make a procedurally generated system of values like this, using equations instead of tables, was that I had something like 5 or 6 variables in an equation, and, while it technically is possible to generate equations from as many variables as you want, the number of data points you need to give your function to approximate functions/behaviors that seem reasonable jumps extremely quickly.
Why having one function to rule them all is a bad idea:
I only needed 3 or 4 data points to get really nice, behaved functions that did exactly what I wanted for every possible value here, but you need hundreds (or more) data points to get 4 or 5 variable functions to have the level of precision that you need, and even then the parameters will start interacting in really funky ways and it may just not work at all.
How you can avoid it:
Honestly, guess some realistic values and hard-code them into the game. I decided arbitrarily that the player should need to find 2/3 of the loot on the level in order to be able to afford cool new stuff. That could have been a variable, and if it was it would have ruined my day.
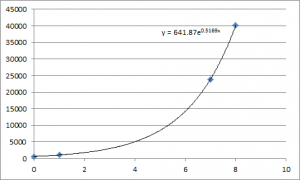
If we were doing this as a Facebook game and selling these items through microtransactions rather than giving them away for free in our dungeon, then the curve of your chart would be displaying our company revenue over time.
Sure, if you think that the number of players is a constant, and their level is linearly increasing. Are those good assumptions?
After reading this am I right in thinking that the precision of the graph allows for less data points to be placed along the line for the function or is this more quirky humour in that the value could be rounded but is not?